Mục lục
Phần I: Giới Thiệu và Đặt Vấn Đề
1. Mở Đầu
Bộ lọc Kalman (Kalman Filter - KF), được đặt theo tên của Rudolf E. Kálmán, là một thuật toán đệ quy mạnh mẽ được sử dụng để ước lượng trạng thái nội tại của một hệ thống động tuyến tính từ một loạt các phép đo không hoàn hảo và chứa nhiễu. Nói một cách đơn giản, nó là một công cụ tối ưu thống kê để kết hợp thông tin từ nhiều nguồn không chắc chắn (mô hình dự đoán và dữ liệu đo lường) nhằm đưa ra một ước lượng tốt nhất về những gì đang thực sự xảy ra với hệ thống.
Trong bài viết này, chúng ta sẽ cùng nhau “giải phẫu” bộ lọc Kalman. Chúng ta sẽ bắt đầu từ những động lực thúc đẩy sự ra đời của nó, ôn lại các kiến thức toán học nền tảng, sau đó từng bước xây dựng nên thuật toán từ những nguyên lý cơ bản, chứng minh các công thức chính, và cuối cùng là xem xét các ví dụ minh họa cũng như ứng dụng thực tiễn của nó.
2. Động Lực và Nguồn Gốc Lịch Sử
Nhu cầu ước lượng và dự đoán trạng thái của các hệ thống trong điều kiện không chắc chắn đã tồn tại từ lâu trong nhiều lĩnh vực, từ thiên văn học, điều khiển học đến kinh tế. Trước bộ lọc Kalman, các phương pháp như bình phương tối thiểu (Least Squares) của Gauss đã được sử dụng. Tuy nhiên, phương pháp bình phương tối thiểu cổ điển thường là xử lý theo lô (batch processing), yêu cầu toàn bộ tập dữ liệu phải có sẵn để xử lý cùng một lúc. Điều này không phù hợp cho các hệ thống thay đổi theo thời gian (hệ thống động) hoặc khi dữ liệu đến tuần tự.
Bộ lọc Kalman, được giới thiệu bởi Rudolf Kálmán vào năm 1960, đã mang đến một cuộc cách mạng. Nó nổi bật với:
- Tính đệ quy (Recursive): Chỉ cần ước lượng và phép đo ở bước trước đó để tính toán ước lượng hiện tại, không cần lưu trữ toàn bộ lịch sử dữ liệu.
- Tính tối ưu (Optimality): Đối với các hệ thống tuyến tính có nhiễu tuân theo phân phối Gaussian, bộ lọc Kalman cung cấp ước lượng không chệch có phương sai nhỏ nhất (Minimum Mean Square Error - MMSE estimator).
- Xử lý thời gian thực: Phù hợp cho các ứng dụng cần cập nhật ước lượng liên tục.
Ứng dụng nổi tiếng và tiên phong đầu tiên của bộ lọc Kalman là trong chương trình Apollo của NASA, nơi nó được sử dụng để định vị và dẫn đường cho tàu vũ trụ trên hành trình đến Mặt Trăng.
3. Kiến Thức Nền Tảng Cần Thiết
Để hiểu sâu sắc và xây dựng được bộ lọc Kalman, bạn cần nắm vững một số khái niệm toán học:
- Xác suất và Thống kê:
- Biến ngẫu nhiên và Phân phối xác suất: Khái niệm về sự không chắc chắn và cách mô tả nó.
- Phân phối Gaussian (Normal Distribution): Đây là “trái tim” của bộ lọc Kalman chuẩn (linear Kalman filter).
- Một biến ngẫu nhiên vô hướng tuân theo phân phối Gaussian với trung bình (kỳ vọng) và phương sai được ký hiệu là . Hàm mật độ xác suất (PDF) của nó là:
- Đối với vector ngẫu nhiên đa biến , nếu nó tuân theo phân phối Gaussian đa biến với vector kỳ vọng và ma trận hiệp phương sai , ta ký hiệu . Hàm PDF có dạng:
-
Kỳ vọng (Mean / Expected Value):
là giá trị trung bình, “tâm” của phân phối. -
Phương sai (Variance):
đo lường mức độ phân tán của biến ngẫu nhiên quanh kỳ vọng của nó. -
Ma trận Hiệp phương sai (Covariance Matrix):
Đối với vector ngẫu nhiên đa biến , ma trận hiệp phương sai
có các phần tử trên đường chéo chính là phương sai của từng thành phần trong ,
và các phần tử ngoài đường chéo chính là hiệp phương sai giữa các cặp thành phần, thể hiện mức độ tương quan tuyến tính giữa chúng. -
Tính chất của kỳ vọng và phương sai:
- Nếu và độc lập:
-
Đại số tuyến tính:
- Phép toán ma trận: cộng, trừ, nhân, chuyển vị (transpose), nghịch đảo (inverse).
- Vector, không gian vector, cơ sở.
- Định thức (determinant) của ma trận.
-
Hệ thống động (Dynamical Systems):
- Khái niệm về trạng thái của một hệ thống.
- Mô hình không gian trạng thái (state-space representation) để mô tả sự tiến triển của trạng thái theo thời gian.
Phần II: Xây Dựng Mô Hình Toán Học
Bộ lọc Kalman hoạt động dựa trên việc mô tả hệ thống bằng hai phương trình chính, biểu diễn dưới dạng không gian trạng thái. Chúng ta giả định rằng cả nhiễu quá trình và nhiễu đo lường đều là nhiễu trắng Gaussian, không tương quan với nhau và không tương quan với trạng thái.
1. Mô Tả Hệ Thống Động Tuyến Tính Rời Rạc
a. Mô hình Quá trình (Process Model hay State Transition Model)
Phương trình này mô tả cách trạng thái của hệ thống tại thời điểm (rời rạc) tiến triển từ trạng thái ở thời điểm trước đó :
Trong đó:
- : Vector trạng thái tại thời điểm . Ví dụ: vị trí, vận tốc, gia tốc của một đối tượng.
- : Ma trận chuyển đổi trạng thái (state transition matrix) từ sang . Nó mô tả động lực học nội tại của hệ thống.
- : Vector đầu vào điều khiển (control input vector) tại thời điểm (nếu có). Ví dụ: lực tác động lên một robot.
- : Ma trận điều khiển đầu vào (control input matrix). Nó liên kết đầu vào điều khiển với trạng thái.
- : Vector nhiễu quá trình (process noise vector) tại . Đây là một vector ngẫu nhiên Gauss đa biến, giả định là nhiễu trắng với kỳ vọng bằng không và ma trận hiệp phương sai : Nhiễu quá trình thể hiện sự không chắc chắn trong mô hình động của chúng ta, hoặc các yếu tố ngoại cảnh không được mô hình hóa. Ví dụ, nếu theo dõi một chiếc xe, có thể đại diện cho những thay đổi gia tốc không lường trước do gió, mặt đường không bằng phẳng, hoặc sai số trong mô hình động lực học của xe.
b. Mô hình Đo lường (Measurement Model)
Phương trình này mô tả mối quan hệ giữa trạng thái thực và phép đo mà chúng ta thu được từ các cảm biến tại thời điểm :
Trong đó:
- : Vector đo lường tại thời điểm . Ví dụ: vị trí đo được từ GPS, góc đo từ radar.
- : Ma trận đo lường (measurement matrix hoặc observation matrix). Nó liên kết trạng thái thực với không gian đo lường.
- : Vector nhiễu đo lường (measurement noise vector) tại . Đây cũng là một vector ngẫu nhiên Gauss đa biến, giả định là nhiễu trắng với kỳ vọng bằng không và ma trận hiệp phương sai : Nhiễu đo lường thể hiện sự không chính xác và nhiễu cố hữu của các cảm biến.
Các giả định quan trọng:
- Nhiễu quá trình và nhiễu đo lường là độc lập thống kê với nhau.
- Chúng cũng độc lập với trạng thái ban đầu .
- Chúng là các chuỗi nhiễu trắng (uncorrelated in time).
2. Mục Tiêu Ước Lượng
Mục tiêu của chúng ta là tìm ra ước lượng “tốt nhất” cho trạng thái thực ẩn dựa trên tất cả các thông tin có sẵn cho đến thời điểm . Ký hiệu:
- : Ước lượng trạng thái tiên nghiệm (a priori state estimate) tại thời điểm , dựa trên các phép đo đến thời điểm . Đây là dự đoán của chúng ta về trạng thái tại trước khi có phép đo mới .
- : Ước lượng trạng thái hậu nghiệm (a posteriori state estimate) tại thời điểm , dựa trên các phép đo đến thời điểm (bao gồm cả ). Đây là ước lượng được hiệu chỉnh sau khi đã kết hợp thông tin từ phép đo mới.
“Tốt nhất” ở đây thường được hiểu theo nghĩa là tối thiểu hóa phương sai của sai số ước lượng (Minimum Mean Square Error - MMSE). Trong trường hợp nhiễu Gaussian, ước lượng MMSE cũng chính là kỳ vọng có điều kiện của trạng thái.
Cùng với ước lượng trạng thái, chúng ta cũng cần ước lượng độ không chắc chắn của các ước lượng đó, được biểu diễn bởi các ma trận hiệp phương sai sai số:
- : Ma trận hiệp phương sai sai số tiên nghiệm.
- : Ma trận hiệp phương sai sai số hậu nghiệm.
Các phần tử trên đường chéo của cho biết phương sai (độ không chắc chắn) của từng thành phần trạng thái, và các phần tử ngoài đường chéo cho biết hiệp phương sai (mức độ tương quan sai số) giữa các cặp thành phần. Mục tiêu là làm cho các phần tử của càng nhỏ càng tốt.
Phần III: Xây Dựng và Chứng Minh Thuật Toán Bộ Lọc Kalman
Bộ lọc Kalman hoạt động theo một chu trình đệ quy gồm hai bước chính: Dự đoán (Prediction), còn gọi là Cập nhật Thời gian (Time Update), và Hiệu chỉnh (Correction), còn gọi là Cập nhật Đo lường (Measurement Update).
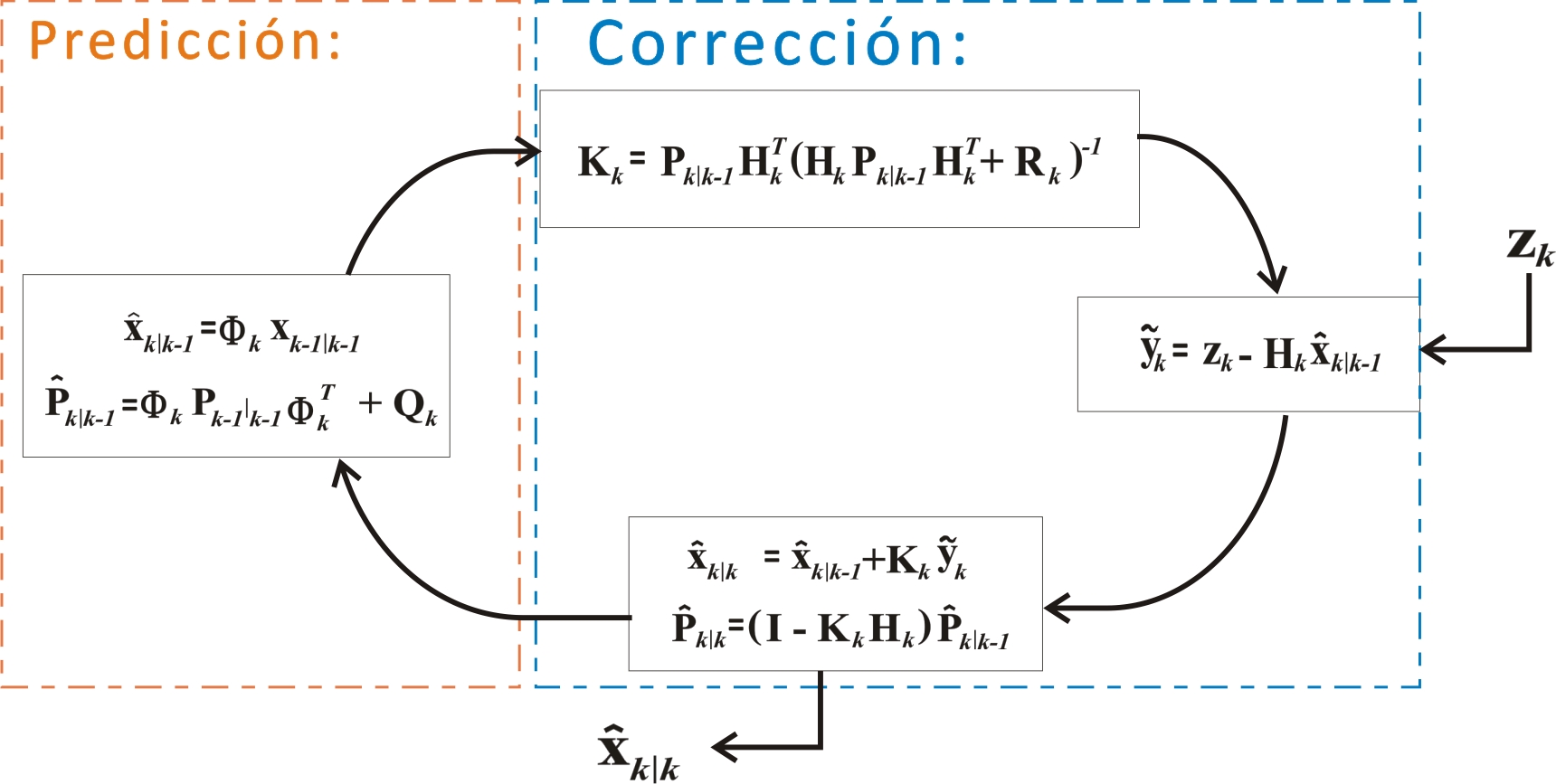
1. Bước Dự Đoán (Time Update)
Ở bước này, chúng ta dự đoán trạng thái và hiệp phương sai sai số tại thời điểm dựa trên thông tin từ thời điểm . Giả sử chúng ta đã có ước lượng hậu nghiệm và hiệp phương sai từ bước trước.
a. Dự đoán trạng thái tiên nghiệm ()
Chúng ta sử dụng mô hình quá trình để dự đoán trạng thái:
Chứng minh: Lấy kỳ vọng của phương trình mô hình quá trình , có điều kiện là tất cả các phép đo đến (ký hiệu ): Vì là nhiễu trắng có kỳ vọng bằng 0 và độc lập với các phép đo quá khứ, . Do đó: .
b. Dự đoán hiệp phương sai sai số tiên nghiệm ()
Sai số dự đoán tiên nghiệm là: . .
Hiệp phương sai: .
Vì sai số và nhiễu quá trình là độc lập và có kỳ vọng bằng không, các số hạng chéo (cross terms) sẽ bằng không khi lấy kỳ vọng. (vì nếu ước lượng là không chệch). Do đó:
(Lưu ý: một số tài liệu dùng thay vì , tùy thuộc vào quy ước chỉ số thời gian của nhiễu).
2. Bước Hiệu Chỉnh (Measurement Update)
Khi có phép đo mới , chúng ta sử dụng nó để hiệu chỉnh ước lượng tiên nghiệm thành ước lượng hậu nghiệm . Ý tưởng cơ bản là kết hợp tuyến tính giữa dự đoán tiên nghiệm và thông tin từ phép đo mới:
Trong bộ lọc Kalman, dạng cụ thể hơn là:
Term được gọi là innovation hoặc measurement residual (phần dư đo lường), ký hiệu là . Nó biểu diễn sự khác biệt giữa phép đo thực tế và phép đo dự kiến (dựa trên dự đoán trạng thái tiên nghiệm). Ma trận được gọi là Kalman Gain. Nó quyết định mức độ chúng ta “tin tưởng” vào phép đo mới (innovation) so với dự đoán tiên nghiệm. Nếu nhỏ, chúng ta tin vào dự đoán nhiều hơn. Nếu lớn, chúng ta tin vào phép đo nhiều hơn.
a. Tính toán Kalman Gain ()
Mục tiêu là chọn sao cho phương sai của sai số ước lượng hậu nghiệm là nhỏ nhất. Điều này tương đương với việc tối thiểu hóa trace (tổng các phần tử trên đường chéo chính) của .
Sai số hậu nghiệm:
Thay :
Hiệp phương sai sai số hậu nghiệm:
Vì (dựa trên đến ) và (nhiễu đo lường tại ) là độc lập và có kỳ vọng bằng không, các số hạng chéo sẽ bằng không:
Đây là dạng Joseph (Joseph form) của phương trình cập nhật hiệp phương sai, nó ổn định hơn về mặt số học.
Để tìm tối ưu, ta lấy đạo hàm của trace của theo và đặt bằng 0.
Lấy đạo hàm theo (sử dụng các quy tắc đạo hàm ma trận) ta có:
Giải phương trình này cho ta được:
Ma trận được gọi là ma trận hiệp phương sai innovation (innovation covariance matrix), ký hiệu .
Vậy:
b. Cập nhật ước lượng trạng thái hậu nghiệm ()
Như đã nêu ở trên:
c. Cập nhật hiệp phương sai sai số hậu nghiệm ()
Thay vào dạng Joseph của ở trên là một cách. Một dạng phổ biến và đơn giản hơn (dù có thể kém ổn định số học hơn dạng Joseph trong một số trường hợp): Từ định nghĩa , ta có . Vậy . Thay vào: . Đây là dạng đơn giản và thường được sử dụng.
3. Khởi Tạo
Để bắt đầu chu trình đệ quy, chúng ta cần cung cấp:
- Ước lượng trạng thái ban đầu:
- Ma trận hiệp phương sai sai số ban đầu:
Nếu chúng ta không có thông tin chính xác về trạng thái ban đầu, có thể được đặt là một giá trị hợp lý (ví dụ, dựa trên phép đo đầu tiên hoặc bằng không). nên được đặt với các giá trị lớn trên đường chéo chính (thể hiện độ không chắc chắn ban đầu cao), và các giá trị ngoài đường chéo bằng không nếu không có thông tin về tương quan sai số ban đầu. Bộ lọc Kalman có xu hướng hội tụ về ước lượng đúng ngay cả khi giá trị khởi tạo không quá chính xác, miễn là hệ thống có thể quan sát được (observable).
Phần IV: Kết Luận
Bộ lọc Kalman là một công cụ mạnh mẽ cho ước lượng trạng thái tối ưu trong các hệ thống động tuyến tính với nhiễu Gaussian...
Phần V: Ví Dụ Minh Họa - Theo dõi Chuyển Động 1D
Hãy xem xét một ví dụ theo dõi vị trí và vận tốc của một đối tượng chuyển động trên một đường thẳng với gia tốc ngẫu nhiên nhỏ.
- Trạng thái: , với là vị trí và là vận tốc tại thời điểm .
- Mô hình quá trình: Giả sử chuyển động với vận tốc gần như không đổi trong khoảng thời gian nhỏ , nhưng có thể bị tác động bởi gia tốc ngẫu nhiên. Nhiễu quá trình liên quan đến gia tốc ngẫu nhiên . Ma trận . Ma trận (nếu có điều khiển) hoặc cách mô hình hóa nhiễu quá trình sẽ phụ thuộc vào giả định về . Một cách phổ biến là mô hình hóa nhiễu gia tốc liên tục: , với là phương sai của nhiễu gia tốc.
- Mô hình đo lường: Giả sử chúng ta chỉ đo được vị trí với nhiễu. Ma trận . Ma trận (scalar trong trường hợp này, với là phương sai nhiễu đo vị trí).
Code Python (NumPy)
(Phần code Python bạn cung cấp cho ví dụ theo dõi vị trí 1D là rất tốt và trực quan. Tôi sẽ giữ nguyên nó và chỉ bổ sung một vài chú thích để làm rõ hơn mối liên hệ với các công thức đã chứng minh).
import numpy as npimport matplotlib.pyplot as plt
class KalmanFilter: def __init__(self, A, B, H, Q, R, x0, P0): self.A = A # Ma trận chuyển đổi trạng thái self.B = B # Ma trận điều khiển (có thể là None nếu không có u_k) self.H = H # Ma trận đo lường self.Q = Q # Hiệp phương sai nhiễu quá trình (cho wk) self.R = R # Hiệp phương sai nhiễu đo lường (cho vk)
self.x_hat = x0 # Ước lượng trạng thái ban đầu (x_0|0) self.P = P0 # Hiệp phương sai sai số ban đầu (P_0|0)
def predict(self, u=None): """Bước Dự Đoán (Time Update)""" # Dự đoán trạng thái tiên nghiệm: x_hat_k|k-1 = A @ x_hat_k-1|k-1 (+ B @ u_k) if self.B is not None and u is not None: self.x_hat_apriori = self.A @ self.x_hat + self.B @ u else: self.x_hat_apriori = self.A @ self.x_hat
# Dự đoán hiệp phương sai sai số tiên nghiệm: P_k|k-1 = A @ P_k-1|k-1 @ A.T + Q self.P_apriori = self.A @ self.P @ self.A.T + self.Q
# Lưu lại để dùng ở bước cập nhật self.x_hat = self.x_hat_apriori self.P = self.P_apriori
def update(self, z): """Bước Hiệu Chỉnh (Measurement Update)""" # Tính innovation (measurement residual): y_tilde_k = z_k - H @ x_hat_k|k-1 y_tilde = z - self.H @ self.x_hat_apriori
# Tính hiệp phương sai innovation: S_k = H @ P_k|k-1 @ H.T + R S = self.H @ self.P_apriori @ self.H.T + self.R
# Tính Kalman Gain: K_k = P_k|k-1 @ H.T @ inv(S_k) K = self.P_apriori @ self.H.T @ np.linalg.inv(S)
# Cập nhật ước lượng trạng thái hậu nghiệm: x_hat_k|k = x_hat_k|k-1 + K_k @ y_tilde_k self.x_hat = self.x_hat_apriori + K @ y_tilde
# Cập nhật hiệp phương sai sai số hậu nghiệm: P_k|k = (I - K_k @ H) @ P_k|k-1 # (Hoặc dạng Joseph để ổn định hơn: P_k|k = (I - K_k @ H) @ P_k|k-1 @ (I - K_k @ H).T + K @ R @ K.T) I = np.eye(self.P_apriori.shape[0]) self.P = (I - K @ self.H) @ self.P_apriori # self.P = (I - K @ self.H) @ self.P_apriori @ (I - K @ self.H).T + K @ self.R @ K.T # Dạng Joseph
# Tham số mô phỏng cho theo dõi vị trí và vận tốc 1Ddt = 0.1 # Bước thời gian (s)n_steps = 200 # Số bước mô phỏngprocess_noise_std = 0.2 # Độ lệch chuẩn của nhiễu gia tốc (m/s^2)measurement_noise_std = 1.0 # Độ lệch chuẩn của nhiễu đo vị trí (m)
# Tạo dữ liệu thực (True states)np.random.seed(42)true_positions = np.zeros(n_steps)true_velocities = np.zeros(n_steps)measurements = np.zeros(n_steps)
# Giá trị ban đầu của hệ thống thựccurrent_pos = 0.0current_vel = 1.0 # m/s
for i in range(n_steps): # Mô phỏng gia tốc ngẫu nhiên (nhiễu quá trình) random_acc = np.random.normal(0, process_noise_std)
# Cập nhật trạng thái thực current_pos = current_pos + current_vel * dt + 0.5 * random_acc * dt**2 current_vel = current_vel + random_acc * dt
true_positions[i] = current_pos true_velocities[i] = current_vel
# Tạo phép đo với nhiễu measurements[i] = current_pos + np.random.normal(0, measurement_noise_std)
# Khởi tạo các ma trận cho Bộ lọc Kalman# Mô hình quá trình: x_k = A * x_{k-1} + w_{k-1} (không có điều khiển B*u)# x = [position, velocity]^TA = np.array([[1, dt], [0, 1]])
# Ma trận H cho mô hình đo lường: z_k = H * x_k + v_k# Chúng ta chỉ đo vị tríH = np.array([[1, 0]])
# Ma trận hiệp phương sai nhiễu quá trình Q# Mô hình hóa nhiễu do gia tốc ngẫu nhiên tác động lên cả vị trí và vận tốc# Q = G * G.T * sigma_a^2, với G = [dt^2/2, dt]^T# Đây là một cách xây dựng Q phổ biến cho mô hình gia tốc không đổi bị nhiễu.G = np.array([[0.5*dt**2], [dt]])Q = G @ G.T * (process_noise_std**2)# Hoặc một dạng đơn giản hơn nếu giả định nhiễu độc lập cho vị trí và vận tốc# Q = np.array([[ (dt**4)/4 * process_noise_std**2 , (dt**3)/2 * process_noise_std**2],# [ (dt**3)/2 * process_noise_std**2 , dt**2 * process_noise_std**2 ]])
# Ma trận hiệp phương sai nhiễu đo lường RR = np.array([[measurement_noise_std**2]])
# Điều kiện ban đầu cho bộ lọcx0_hat = np.array([0.0, 0.0]) # Ước lượng ban đầu về vị trí và vận tốcP0 = np.array([[1.0, 0.0], # Phương sai vị trí ban đầu lớn [0.0, 1.0]]) # Phương sai vận tốc ban đầu lớn
kf = KalmanFilter(A=A, B=None, H=H, Q=Q, R=R, x0=x0_hat, P0=P0)
# Chạy bộ lọc qua các bước thời gianestimated_positions_kf = []estimated_velocities_kf = []P_diagonal_variances = [] # Lưu trữ phương sai (đường chéo của P)
for i in range(n_steps): # Bước dự đoán kf.predict()
# Bước cập nhật với phép đo mới kf.update(np.array([measurements[i]]))
estimated_positions_kf.append(kf.x_hat[0]) estimated_velocities_kf.append(kf.x_hat[1]) P_diagonal_variances.append(np.diag(kf.P))
estimated_positions_kf = np.array(estimated_positions_kf)estimated_velocities_kf = np.array(estimated_velocities_kf)P_diagonal_variances = np.array(P_diagonal_variances)
# Tính toán khoảng tin cậy (ví dụ 95% CI là +/- 1.96 * std_dev)pos_std_dev = np.sqrt(P_diagonal_variances[:, 0])vel_std_dev = np.sqrt(P_diagonal_variances[:, 1])
# Trực quan hóa kết quảtime_axis = np.arange(n_steps) * dt
plt.figure(figsize=(16, 12))
plt.subplot(2, 1, 1)plt.plot(time_axis, true_positions, 'g-', label='Vị trí Thực', linewidth=2, alpha=0.8)plt.plot(time_axis, measurements, 'ro', label='Đo lường Thô', markersize=4, alpha=0.5)plt.plot(time_axis, estimated_positions_kf, 'b-', label='Ước lượng Vị trí (KF)', linewidth=2)plt.fill_between(time_axis, estimated_positions_kf - 1.96 * pos_std_dev, estimated_positions_kf + 1.96 * pos_std_dev, color='blue', alpha=0.2, label='95% Khoảng Tin Cậy (Vị trí)')plt.xlabel('Thời gian (s)')plt.ylabel('Vị trí (m)')plt.title('Theo dõi Vị trí 1D với Bộ lọc Kalman')plt.legend(loc='upper left')plt.grid(True, linestyle='--', alpha=0.7)
plt.subplot(2, 1, 2)plt.plot(time_axis, true_velocities, 'g-', label='Vận tốc Thực', linewidth=2, alpha=0.8)plt.plot(time_axis, estimated_velocities_kf, 'b-', label='Ước lượng Vận tốc (KF)', linewidth=2)plt.fill_between(time_axis, estimated_velocities_kf - 1.96 * vel_std_dev, estimated_velocities_kf + 1.96 * vel_std_dev, color='blue', alpha=0.2, label='95% Khoảng Tin Cậy (Vận tốc)')plt.xlabel('Thời gian (s)')plt.ylabel('Vận tốc (m/s)')plt.title('Ước lượng Vận tốc 1D với Bộ lọc Kalman')plt.legend(loc='upper left')plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()plt.show()
# Tính toán lỗi RMS (Root Mean Square Error)position_rmse_kf = np.sqrt(np.mean((estimated_positions_kf - true_positions)**2))velocity_rmse_kf = np.sqrt(np.mean((estimated_velocities_kf - true_velocities)**2))raw_measurement_rmse = np.sqrt(np.mean((measurements - true_positions)**2))
print(f"RMSE Vị trí (Bộ lọc Kalman): {position_rmse_kf:.4f} m")print(f"RMSE Vận tốc (Bộ lọc Kalman): {velocity_rmse_kf:.4f} m/s")print(f"RMSE Đo lường Thô (so với vị trí thực): {raw_measurement_rmse:.4f} m")